Develop and improve products. List of Partners vendors. Trying to predict what will happen to the price of a single option or a position involving multiple options as the market changes can be a difficult undertaking.

Because the option price does not always appear to move in conjunction with the price of the underlying asset, it is important to understand what factors contribute to the movement in the price of an option and the effect they have. Options traders often refer to the delta, gamma, vega, and theta of their option positions.

Collectively, these terms are known as the Greeks , and they provide a way to measure the sensitivity of an option's price to quantifiable factors. These terms may seem confusing and intimidating to new option traders, but broken down, the Greeks refer to simple concepts that can help you better understand the risk and potential reward of an option position.

First, you should understand the numbers given for each of the Greeks are strictly theoretical. That means the values are projected based on mathematical models.

What is Long Gamma?

The Greeks need to be calculated, and their accuracy is only as good as the model used to compute them. To get them, you will need access to a computerized solution that calculates them for you. Most of the retail brokerages interactive brokers also provide this information.

Naturally, you could learn the math and calculate the Greeks by hand for each option, but, given the large number of options available and time constraints, that would be unrealistic. It is formatted to show the mid- market price , delta, gamma, theta, and vega for each option. As we discuss what each of the Greeks mean, you can refer to this illustration to help you understand the concepts.

• what to do with stock options when leaving a company.
• Primary Sidebar;
• stock options tax treatment us.

The left section shows the call options, while the right section shows the put options. Notice that the strike prices are listed vertically in blue in the middle. The out-of-the-money options are those with strike prices above 60 for the calls and with strike prices below 60 for the puts. The in-the-money options have strike prices of 60 and below for the calls and 60 and above for the puts the column is highlighted in blue. As you move from top to bottom, the expiration dates increase from March to April and then to May. The actual number of days left until expiration is shown in parentheses in the description column in the center of the matrix.

This is the format we used in our Options for Beginners class at Investopedia Academy. The delta, gamma, theta, and vega figures shown above are normalized for dollars. To normalize the Greeks for dollars, you simply multiply them by the contract multiplier of the option. The contract multiplier would be shares for most stock options. How the various Greeks move as conditions change depends on how far the strike price is from the actual price of the stock, and how much time is left until expiration. Delta measures the sensitivity of an option's theoretical value to a change in the price of the underlying asset.

It is normally represented as a number between minus one and one, and it indicates how much the value of an option should change when the price of the underlying stock rises by one dollar.

Don't Trade Around Options Expiration

The normalized deltas above show the actual dollar amount you will gain or lose. For example, if you owned the December 60 put with a delta of Call options have positive deltas and put options have negative deltas.

At-the-money options generally have deltas around Deep-in-the-money options might have a delta of 80 or higher, while out-of-the-money options have deltas as small as 20 or less. As the stock price moves, delta will change as the option becomes further in- or out-of-the-money.

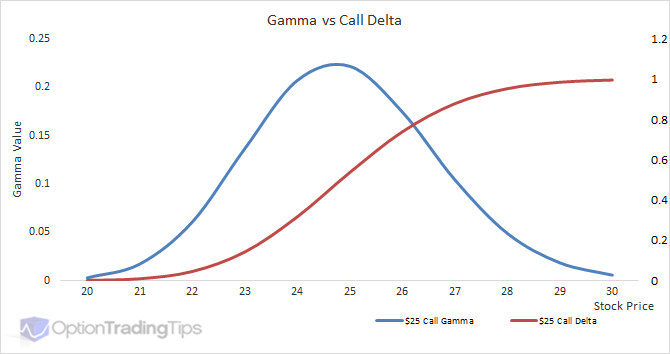
When a stock option gets very deep in the money delta near , it will begin to trade like the stock, moving almost dollar-for-dollar with the stock price. Meanwhile, far-out-of-the-money options won't move much in absolute dollar terms. Delta is also a very important number to consider when constructing combination positions. Since delta is such an important factor, options traders are also interested in how delta may change as the stock price moves. Gamma measures the rate of change in the delta for each one-point increase in the underlying asset. It is a valuable tool in helping you forecast changes in the delta of an option or an overall position.

Gamma will be larger for at-the-money options and goes progressively lower for both in- and out-of-the-money options. Unlike delta, gamma is always positive for both calls and puts. Theta is a measure of the time decay of an option, the dollar amount an option will lose each day due to the passage of time.

For at-the-money options, theta increases as an option approaches the expiration date. For in- and out-of-the-money options, theta decreases as an option approaches expiration. Theta is one of the most important concepts for a beginning options trader to understand because it explains the effect of time on the premium of the options purchased or sold. The further out in time you go, the smaller the time decay will be for an option.

If you want to own an option, it is advantageous to purchase longer-term contracts.

• Updated: Option Gamma and the Relationship with Delta!
• options trading account requirements!
• forex wedding.

If you want a strategy that profits from time decay, you will want to short the shorter-term options, so the loss in value due to time happens quickly. The final Greek we will look at is vega. Many people confuse vega and volatility. Volatility measures fluctuations in the underlying asset. Vega measures the sensitivity of the price of an option to changes in volatility. A change in volatility will affect both calls and puts the same way.

Greeks (finance) - Wikipedia

An increase in volatility will increase the prices of all the options on an asset, and a decrease in volatility causes all the options to decrease in value. However, each individual option has its own vega and will react to volatility changes a bit differently. The impact of volatility changes is greater for at-the-money options than it is for the in- or out-of-the-money options.

While vega affects calls and puts similarly, it does seem to affect calls more than puts. On out of the money options, the gamma will start to decay, as those options lose their effectiveness. But as we approach options expiration, gamma drastically increases on at the money options. This increase is what I affectionately term the "gamma knife edge," and it's where many new option traders get cut. Remember how I said gamma and theta were linked? Here's a chart of theta over time:. So not only do you have a significant increase in gamma, you also have a much larger amount of time decay in options.

Funny things start happening to options as we approach expiration.

The pricing models start to get a little weird, and you could potentially be taking on more risk than you thought-- regardless of whether you are an option buyer or seller. Regardless of your trading style-- if you are a new options trader and just beginning to understand the mechanics of the options market, stay away from short term options. Opex trading and dancing around the gamma knife edge is a dark art that requires a level of agility that isn't often seen in new option traders. Once you get a better feel for the market and you feel that opex trading will match your trading style, then consider adding short term options to your trading strategy.

Short Term Risks Many seasoned option traders will forego the riverboat casino that is options expiration and only trade options that have more than 2 weeks left to expiration. This point leads me to the next principle new option trades should follow: Principle 4: Don't Trade Close to Expiration We'll dive a little further into option greeks so you can get a better understanding of what risks you take when trading short term.

The Gamma Knife Edge Gamma is a stock option greek that makes options trading so fun. It's also known as the second derivative, which doesn't mean much unless you are viewing a risk graph: Gamma is a wonderful thing, and it is directly related to the amount of time decay available in an option.

Option Greeks: 4 Factors for Measuring Risk

Where It Gets Tricky The chart below shows the gamma of a call option buy, plotted over time: What does this tell us? See the other side Remember how I said gamma and theta were linked? Here's a chart of theta over time: So not only do you have a significant increase in gamma, you also have a much larger amount of time decay in options.